How do you simulate a living system—one that learns, adapts, and evolves in real time—without being crushed by complexity?
Introduction: The Challenge of “Living” Computation
The more alive our models become, the more demanding they are to compute.
- Every relationship may change at every step.
- Time itself adapts, sometimes speeding up, sometimes slowing down.
- Networks, contexts, and rules evolve together, creating a multidimensional web of updates.
To keep pace, DAM X leverages advanced computational techniques—borrowing from data science, statistics, physics, and computer engineering.
Monte Carlo Simulation: Sampling Complexity
When direct calculation is impossible, Monte Carlo simulation offers a lifeline:
- Instead of solving equations analytically, sample possible futures and average the results.
- Especially useful for modeling uncertainty, rare events, and high-dimensional systems.
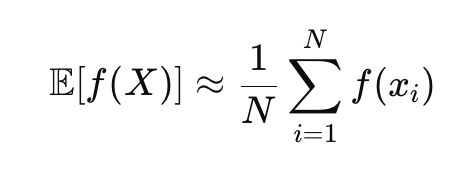
where each xixi is sampled from the distribution of XX.
Importance Sampling:
To efficiently estimate rare but important outcomes:
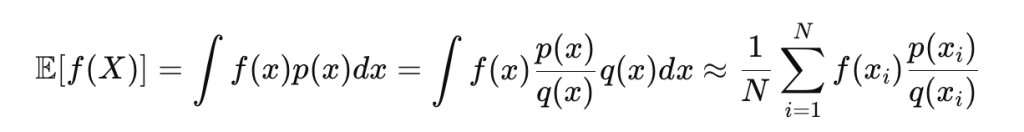
where q(x)q(x) is a proposal distribution focused on important regions.
Markov Chain Monte Carlo (MCMC): Navigating Impossible Spaces
When even Monte Carlo struggles, MCMC shines:
- It builds a “chain” of states, where each new sample depends on the previous one.
- Over time, the chain explores the full probability landscape, even if the space is vast or oddly shaped.
Key algorithms:
- Metropolis-Hastings: Proposes new states, accepts or rejects based on probability.
- Gibbs Sampling: Updates one variable at a time, conditioned on the others.
DAM X uses MCMC to sample from high-dimensional joint distributions—critical for dynamic networks, time-varying copulas, and evolving rules.
Variational Inference: Trading Exactness for Speed
Sometimes, exact sampling is too slow.
Variational inference turns the inference problem into an optimization problem:
- Propose a simple family of distributions q(θ∣ϕ).
- Optimize parameters ϕ to make qq as close as possible to the true distribution p(θ∣D), typically by minimizing KL divergence.
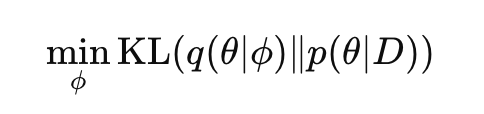
- Fast, scalable, and ideal for online or streaming updates.
- Supported by automatic differentiation tools (e.g., PyTorch, TensorFlow).
Parallel and GPU-Accelerated Computation
DAM X is designed for scale.
- Data parallelism: Split data into chunks, process in parallel.
- Task parallelism: Run different computations (e.g., updating copulas, rules, or network states) in parallel.
- GPU acceleration: Massive speedups for linear algebra, deep learning, and high-dimensional sampling.
Example: Parallel Batch Copula Calculation
python
import torch
def batch_gaussian_copula(u, Sigma, batch_size=1000):
norm_quantiles = torch.distributions.Normal(0, 1).icdf(u).to('cuda')
return multivariate_normal_cdf(norm_quantiles, Sigma.to('cuda'))Dimensionality Reduction: Taming High Dimensions
Big data means high dimensions—millions of features, thousands of entities.
DAM X uses:
- PCA (Principal Component Analysis): Projects data into a smaller number of orthogonal axes.
- t-SNE / MDS: For nonlinear, visualization-friendly embeddings.
PCA Example:
X′=XW
where W is the matrix of eigenvectors of the covariance matrix.
Automatic Model Selection and Hyperparameter Optimization
In living models, the best strategy today may not be best tomorrow.
- DAM X can automatically select among model families (Gaussian copula, t-copula, vine copula, etc.).
- Bayesian optimization or grid/random search for hyperparameters.
- Online evaluation of performance, with adaptation as necessary.
Runtime Optimization and Bottleneck Detection
- Profiling: Identifies bottlenecks (memory, computation).
- Adaptive algorithm selection: If a component is too slow, DAM X can switch to an approximate or parallel version.
- Online resource management: Allocates more power to the most dynamic or important parts of the system.
Practical Example: Real-Time Adaptive Portfolio Simulation
Imagine a portfolio manager using DAM X to monitor 1,000 assets, each with adaptive relationships and changing risk profiles:
- Monte Carlo for scenario generation.
- MCMC for modeling extreme joint events.
- GPU-accelerated covariance updates in real time.
- Automatic risk model selection based on current market regime.
Results:
- Faster risk estimation, even as relationships change.
- Early warning signals for systemic events.
- Scalable computation—from a laptop to a supercomputer.
Why Efficient Computation Matters for Living Models
A living model is only as useful as its ability to keep up with the world.
- Speed enables real-time adaptation.
- Scalability supports richer, more realistic systems.
- Flexibility ensures the model never gets stuck in old routines.
To model life, our mathematics must move as fast as life itself—sometimes faster.